
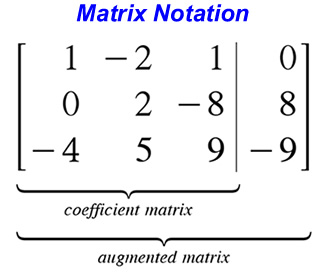
Systems of Linear Equations
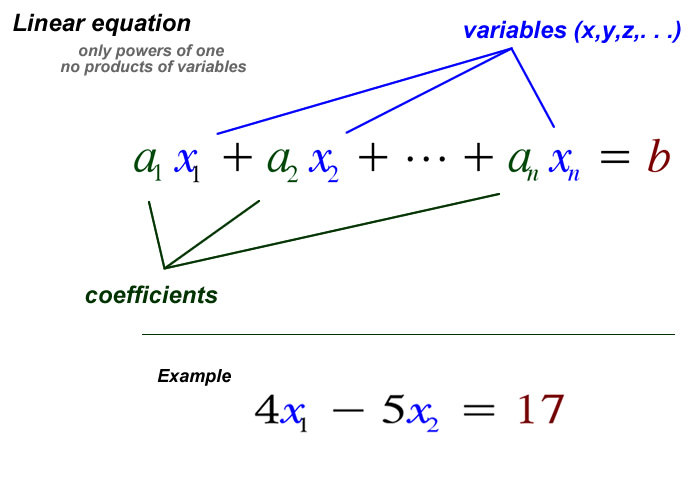
A System of Linear Equations
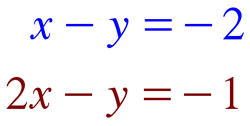
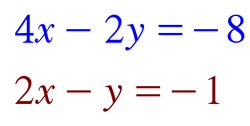
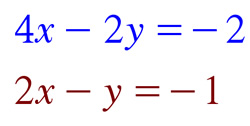
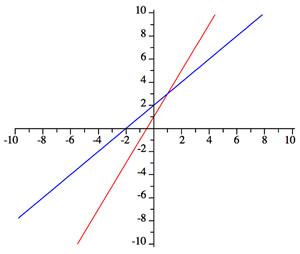
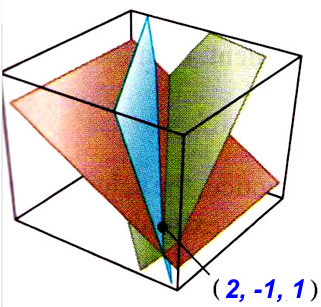
there is no solution
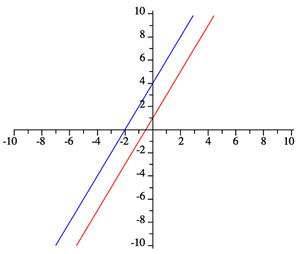
the solution is unique (1,3)
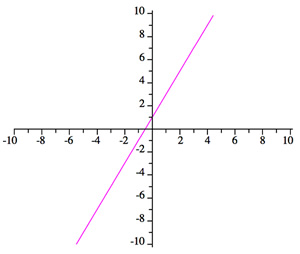
there are infinite solutions
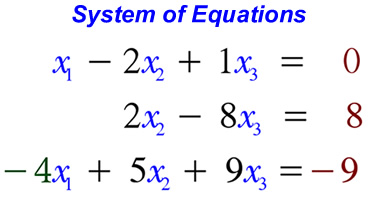
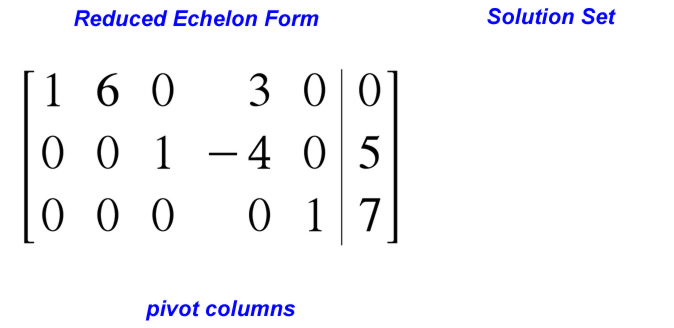
'getting the Matrix in echelon or reduced echelon form'
By applying these 3 Elementary Row Operations to our Matrix we will find a solution, if one exists.
1. (Replacement) Replace one row by the sum of itself and a multiple of another row.
2. (Interchange) Interchange two rows.
3. (Scaling) Multiply all entries of a row by a nonzero constant.


Chapter 1 Sec 2 Problems 8, 9

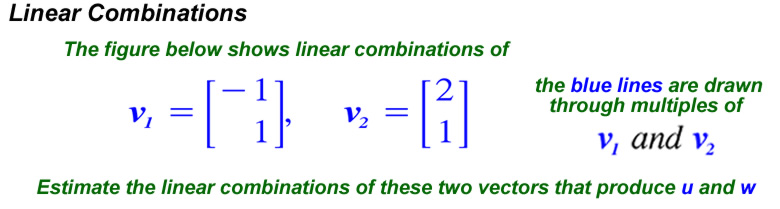
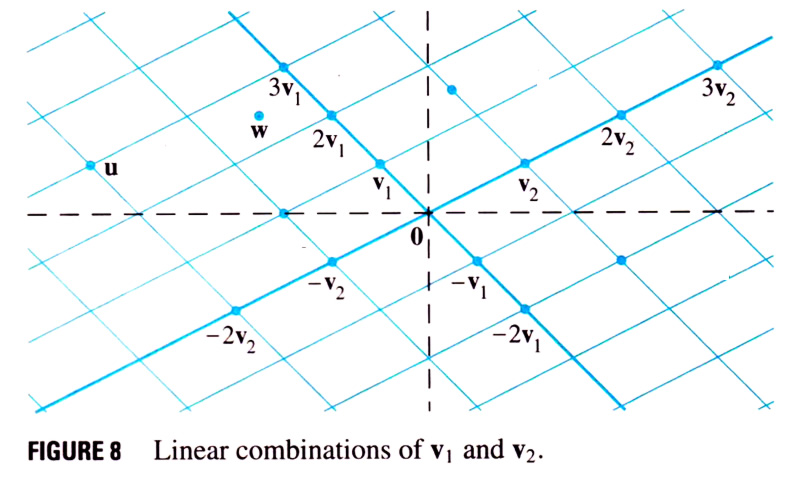

Grapher
Chapter 1 Section 1.3 Problems 17, 18, 25, 26
The Matrix Equation Ax = b
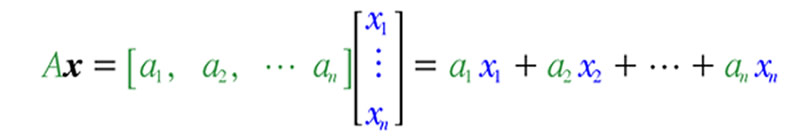
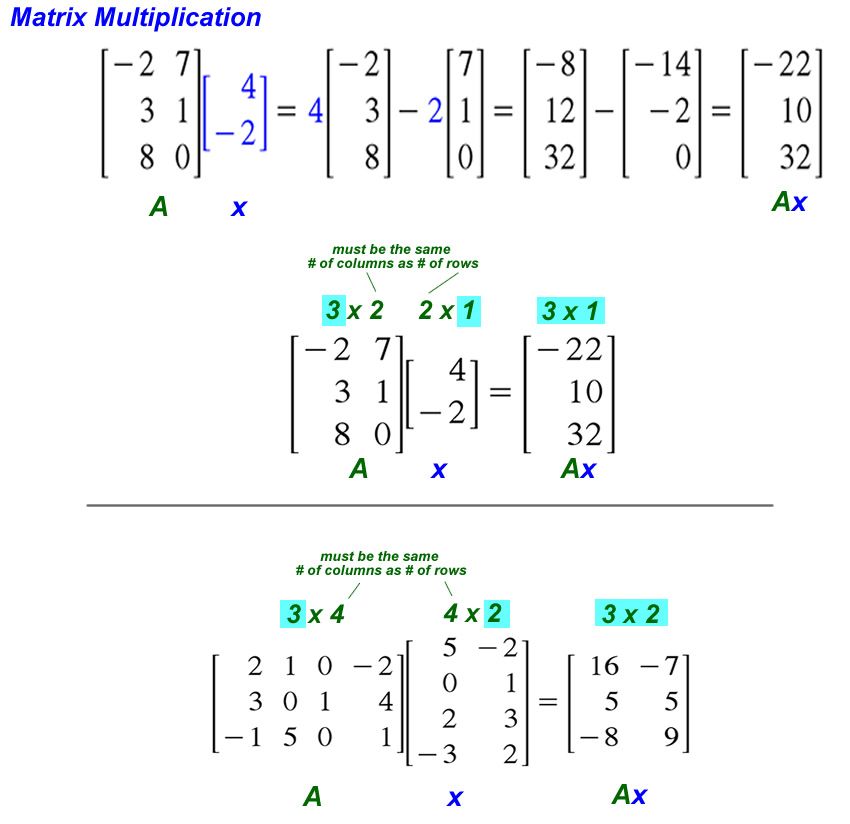


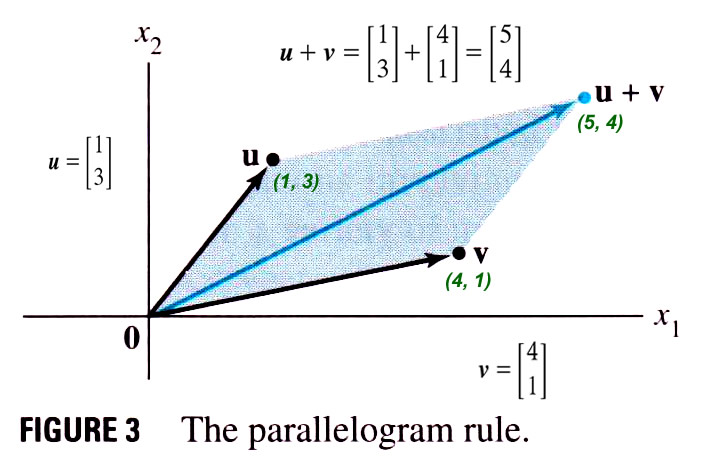
linear combination of the columns of A
The Homogeneous equation Ax = 0 has a nontrivial solution if and only if
the equation has at least one free variable.

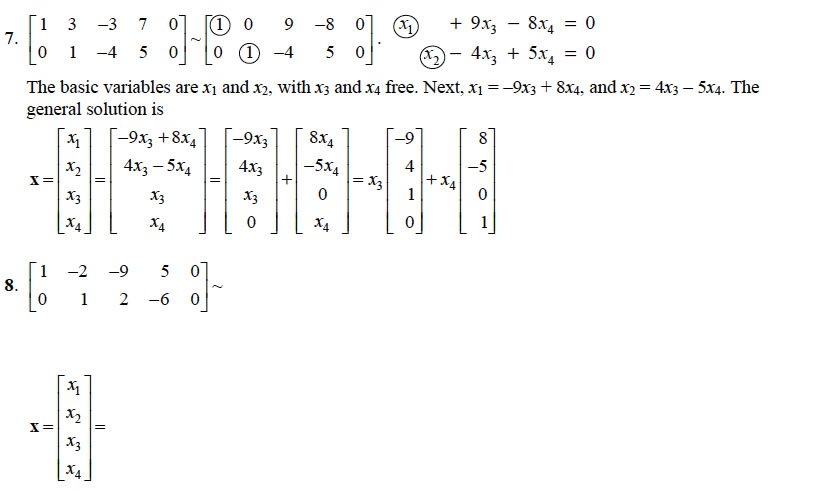
Suppose Ax = b has a solution, explain why the solution is unique
when Ax = 0 has only the trivial solution.
(Geometric argument using Theorem 6.) Since Ax = b is consistent, its solution set is obtained by
translating the solution set of Ax = 0, by Theorem 6. So the solution set of Ax = b is a single vector if
and only if the solution set of Ax = 0 is a single vector, and that happens if and only if Ax = 0 has only
the trivial solution.
(Proof using free variables.) If Ax = b has a solution, then the solution is unique if and only if there
are no free variables in the corresponding system of equations, that is, if and only if every column of A is
a pivot column. This happens if and only if the equation Ax = 0 has only the trivial solution.